CMSC330

RE: describes a set of strings

Context Free Grammars (CFGs): describes a set of strings but more of them

CF Languages more expressive than Regular Languages: can solve more types of problems

Grammar: structure of a langauge

Here is a Grammar for a Regular expression

\(\begin{array}{rl} R \rightarrow & \emptyset\\ & \vert \epsilon\\ & \vert \sigma \\ & \vert R_1R_2\\ & \vert R_1\vert R_2\\ & \vert R_1^*\\ \end{array} \)

Things we need for a CFG

• \(\sum\): Alphabet (known as terminals)
• Non-Terminals: Denotes groups of terminals
• Productions: Says what symbols can replace others
• Start Symbol: where to start

Consider the simple grammar for /[01]+/

Consider the simple grammar for /[01]+/

\(S \rightarrow 0S \vert 1S \vert 1 \vert 0\vert\epsilon\)

If I want to generate the string "001"

\(S \Rightarrow 0S\)

\(0S \Rightarrow 00S\)

\(00S \Rightarrow 001S\)

\(001S \Rightarrow 001\)

This process is called deriving

Designing Grammars

Recursion allows for repetition

\(S \Rightarrow 0S\vert \epsilon\)

Designing Grammars

Seperate Non-terminals can be used for concatenation

\(S \rightarrow AB\)
\(A \rightarrow hello\)
\(B \rightarrow world\)

Designing Grammars

Unline Regex, we can refer backwards

Start at middle of string and build outward

Notation: \(a^nb^n\)

\(S \rightarrow aSb\vert \epsilon\)

Designing Grammars

Each path in a union can be a Non-terminal

(c|k)l(i|y)(ff|ph)

\(S \rightarrow AlBC\)
\(A \rightarrow c|k\)
\(B \rightarrow i|y\)
\(C \rightarrow ff|ph\)

Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

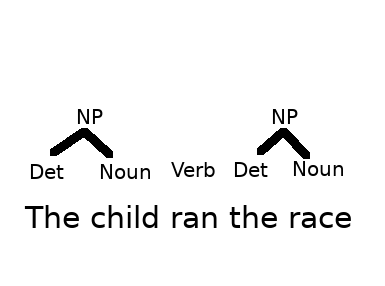
Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

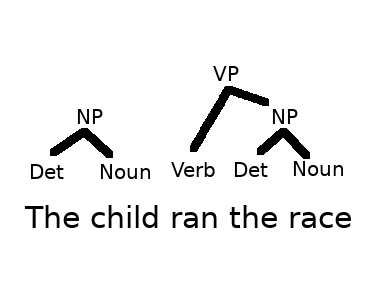
Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

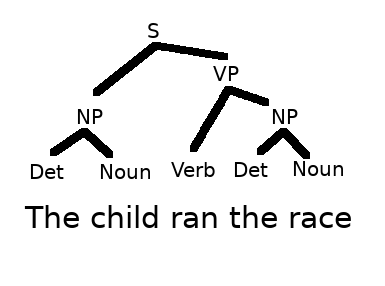
Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

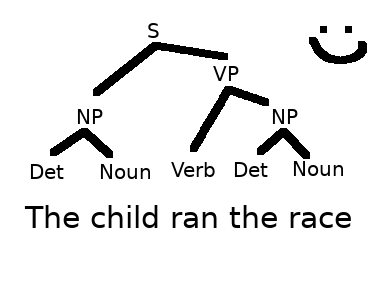
Recall: Grammar describes structure of a langauge

We can model this structure with a Tree

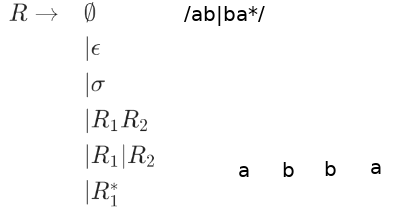
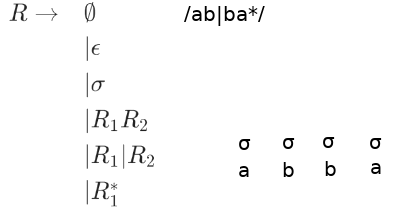
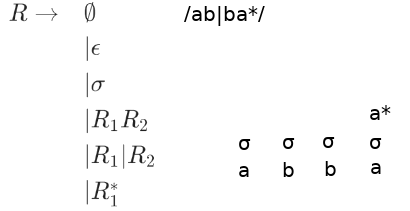
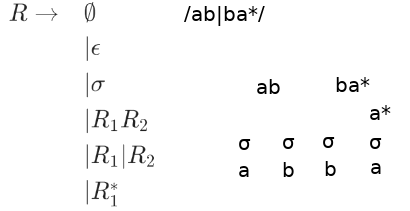
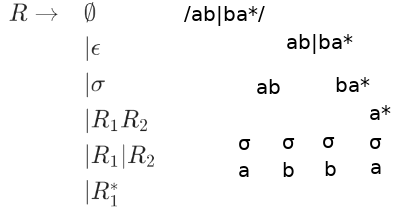
Sometimes multipe trees exist

Conisder the following grammar

\(E \rightarrow A\vert E + E\vert E - E\vert E * E\vert E / E\vert (E)\)
\(A \rightarrow 0\vert 1\vert \dots\vert 9\vert a\vert b\vert \dots \vert z\)

Consider: a - b - c

Consider: a - b - c

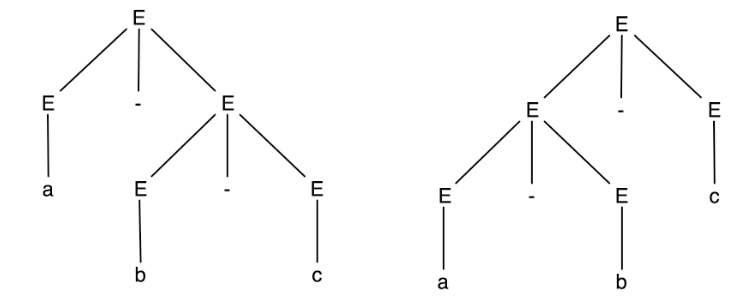
There are left and right derivations

Sometimes, left derivations have multiple deriviations

This is called ambiguity (which is bad)

Two ways to fix ambiguous grammars

• Rewrite the Grammar
• Different Parsers have different rules

Two ways to fix ambiguous grammars

• Rewrite the Grammar
• Ultimately many different ways to describe a set of strings
• Different Parsers have different rules

\(E \rightarrow A\vert E + E\vert E - E\vert E * E\vert E / E\vert (E)\)
\(A \rightarrow 0\vert 1\vert \dots\vert 9\)

Can rewrite the grammar to

\(E \rightarrow \vert E + A\vert E - A\vert E * A\vert E / A\)
\(A \rightarrow 0\vert 1\vert \dots\vert 9\vert (E)\)

No longer Ambiguous, but one problem remains

No longer Ambiguous, but one problem remains

What about precedence?

Parse Trees follow Non-terminals: so add more

\(E \rightarrow E + A\vert E - A\vert A\)
\(A \rightarrow E * B\vert E / B\vert B\)
\(B \rightarrow 0\vert 1\vert \dots\vert 9\vert (E)\)

CFGs can describe programming languages

Will be the basis for parsers

An Abstract Syntax Tree (AST) is the backend data structure parsers use

Basically: parse trees show how things should be parsed

Basically: ASTs are the result of parsing a parse tree