CMSC330

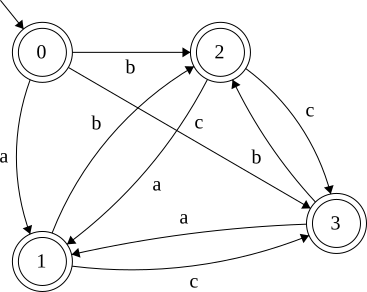
Make a graph to model actions and states of the world

Make a graph to model actions and states of the world

Make a graph to model actions and states of the world

Make a graph to model actions and states of the world

Make a graph to model actions and states of the world

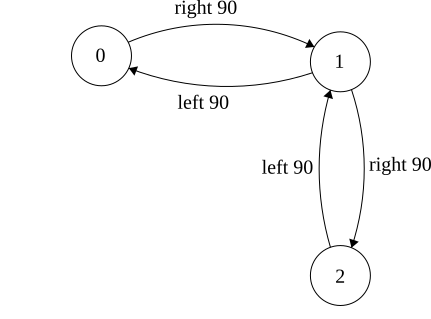
Make a graph to model actions and states of the world

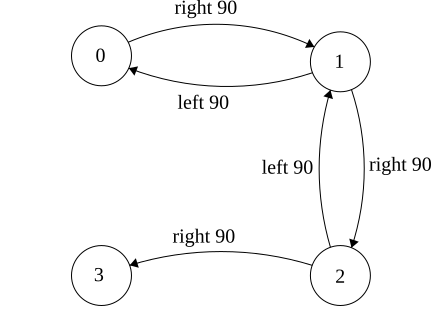
Make a graph to model actions and states of the world

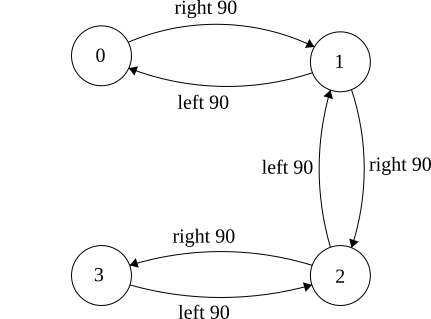
Make a graph to model actions and states of the world

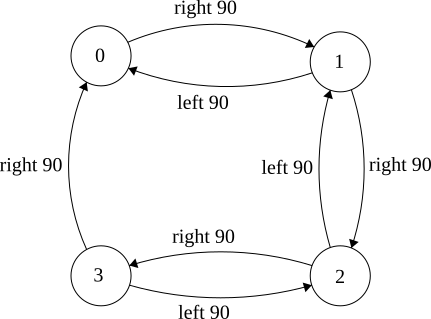
Make a graph to model actions and states of the world

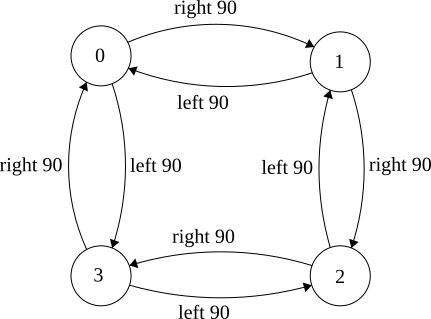
Make a graph to model actions and states of the world

• 0: Face North
• 1: Face East
• 2: Face South
• 3: Face West

Based on where I am, and what I see, go elsewhere

Each Node is a State, and they are finite

Each Node is a State, and they are finite

Basis for Push Down Automata and Turing Machines

Limited operations, but enough for Regex

Recall the things we needed for Regex

• Alphabet
• Concatenation
• Branching
• Repetition

Recall the things we needed for Regex

• Alphabet
• Set of symbols allowed
• Denoted by: \(\sum\)
• String: finite sequence of symbols from \(\sum\)

Recall that a Regex describes a set of strings

This set is called the language

Recall the things we needed for Regex

• Concatenation
• Suppose that \(L_1\) and \(L_2\) are languages
• \(L_1\) concatenated with \(L_2\): \(L_1L_2\)
• \(L_1L_2 = \{xy \vert x \in L_1 \land y \in L_2\}\)

\(L_1 = \{'c'\}, L_2 = \{'m'\}, L_{3} = \{'s'\}\)

\(L_1L_2L_3L_1\) = /cmsc/

Recall the things we needed for Regex

• Branching (Union)
• Suppose that \(L_1\) and \(L_2\) are languages
• \(L_1\) unioned with \(L_2\): \(L_1 \cup L_2\)
• \(L_1 \cup L_2 = \{x \vert x \in L_1 \lor x \in L_2\}\)

\(L_1 = \{'a'\}, L_2 = \{'b'\}, \dots, L_{26} = \{'z'\}\)

\(L_1\cup L_2\cup \dots \cup L_{26}\) = /[a-z]/

\(L_1 = \{'a'\}, L_2 = \{'b'\}, \dots, L_{26} = \{'z'\}\)

\(L_1\cup L_2\cup \dots \cup L_{26}\) = /[a-z]/

\(L_{27} = \{'0'\}, L_{28} = \{'1'\}, \dots, L_{37} = \{'9'\}\)

\((L_1\cup \dots \cup L_{26})(L_{27}\cup \dots \cup L_{37})\) = /[a-z][0-9]/

\(((L_1\cup \dots \cup L_{3})(L_1\cup \dots \cup L_{3}))\cup (L_1\cup \dots \cup L_{3})\) = /[abc]{1,2}/

\(L_{38} = \{'-'\}\)

\((L_{38}(L_{27}\cup \dots \cup L_{37}))\cup (L_{27}\cup \dots \cup L_{37})\) = /-?\d/

\((L_1\cup \dots \cup L_{n})\) = /./

Recall the things we needed for Regex

• Repetition (Kleene closure)
• Suppose that \(L_1\) is a language
• The Kleene Closure of \(L_1\): \(L_1^*\)
• \(L_1^* = \{x|x \in \epsilon \lor x \in L_1 \lor x \in L_1L_1 \lor \dots\}\)

\(L_1 = \{'a'\}\)

\(L_1^*\) = /a*/

\(L_1L_1^*\) = /a+/

We can put everything together to make a grammer

\(\begin{array}{rl} R \rightarrow & \emptyset\\ & \vert \epsilon\\ & \vert \sigma \\ & \vert R_1R_2\\ & \vert R_1\vert R_2\\ & \vert R_1^*\\ \end{array} \)

More on Grammars later

More on Grammars later

Languages created by Regular expressions are regular languages

Suppose \(L\) is a language created by a RE \(r\)

If string \(s \in L\) then \(r\) accepts \(s\)

Not everything can described with Regex

Goal: create a machine to see if \(r\) accepts \(s\)

This machine can be represented by a FSM

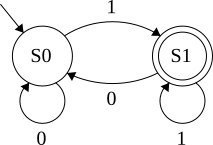
Let's break this down

• Two States: S0, S1
• Initial State: S0
• Accepting State: S1
• Transistions: 0,1

Let's break this down

• Two States: S0, S1
• Initial State: S0
• Can only have 1
• Accepting State: S1
• Transistions: 0,1

Let's break this down

• Two States: S0, S1
• Initial State: S0
• Accepting State: S1
• Can only have zero or more
• Transistions: 0,1

Let's break this down

• Two States: S0, S1
• Initial State: S0
• Accepting State: S1
• Transistions: 0,1
• Denote symbols on an Alphabet

What is this Regex?

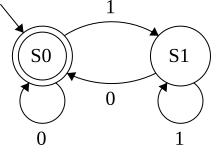
even binary numbers or the empty string

What is this Regex?

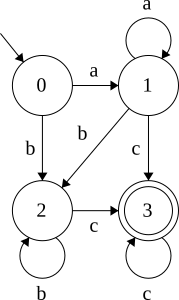
/((a*b+)|(a+b*))c+/

What is this Regex?

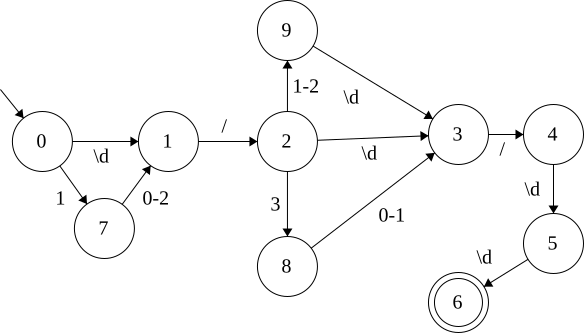
month/day/year Date format

What would this machine look like?

Strings with even number of 0s and odd number of 1s

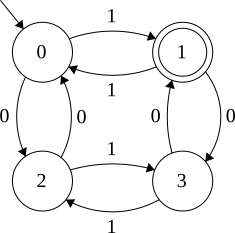
What would this machine look like?

strings of a, b, and c with no same consucutive letters