CMSC250
Logic
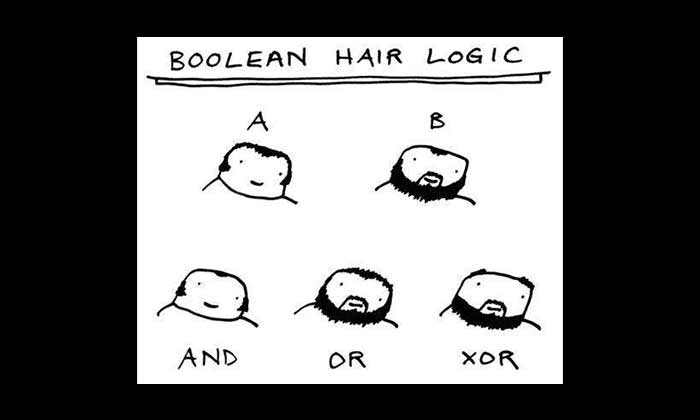
Logic
Arguments
An Argument consists of premises (hypotheses) and a conclusion
An Argument consists of premises (hypotheses) and a conclusion
\[ \begin{array}{rl} & q \\ & p \lor q \\\hline \therefore & p \Rightarrow q \end{array} \]
An Argument consists of premises (hypotheses) and a conclusion
They are typically used to support a claim
An Argument consists of premises (hypotheses) and a conclusion
They are typically used to support a claim
Claim: an assertion of a sentence to be true
Claim: an assertion of a sentence to be true
I am old enough to vote
I like legos
I am old enough to vote
Claims by themselves don't mean much
\[ \begin{array}{rl} & \fragment{2}{\text{I am older than 18}}\\ & \fragment{3}{\text{If you are older than 18, then you can vote}} \\\hline \fragment{4}{\therefore} & \fragment{4}{\text{I can vote}} \end{array} \]
I like legos
\[ \begin{array}{rl} & \fragment{2}{\text{If something brings you joy, you like it}}\\ & \fragment{3}{\text{Legos bring me joy}} \\\hline \fragment{4}{\therefore} & \fragment{4}{\text{I like legos}} \end{array} \]
Validity and Soundness
Arguments can be valid, sound, or neither
An Argument is valid if when the premises are true, the conclusion must also be true
An Argument is valid if when the premises are true, the conclusion must also be true
\[ \begin{array}{c@{\,}l@{}} & q \\ & p \lor q \\\hline \therefore & p \Rightarrow q \end{array} \]
An Argument is valid if when the premises are true, the conclusion must also be true
\[ \begin{array}{c@{\,}l@{}} & q \\ & p \lor q \\\hline \therefore & p \Rightarrow q \end{array} \]
\(([q] \land [p \lor q])\Rightarrow (p \Rightarrow q)\)
\[ \begin{array}{c@{\,}l@{}} & q \\ & p \lor q \\\hline \therefore & p \Rightarrow q \end{array} \]
| \(p\) | \(q\) | \(p \lor q\) | \(p \Rightarrow q\) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
\[ \begin{array}{c@{\,}l@{}} & p \\ & p \lor q \\\hline \therefore & p \Rightarrow q \end{array} \]
| \(p\) | \(q\) | \(p \lor q\) | \(p \Rightarrow q\) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
An Argument is sound if the argument is valid and all premises are actually True
An Argument is sound if the argument is valid and all premises are actually True
\[ \begin{array}{c@{\,}l@{}} & \text{I am older than 18}\\ & \text{If someone older than 18, they are not a teenager}\\\hline \therefore & \text{I am not a teenager} \end{array} \]
An Argument is sound if the argument is valid and all premises are actually True
\[ \begin{array}{c@{\,}l@{}} & \text{I am 18}\\ & \text{If someone is 18, they are a teenager}\\\hline \therefore & \text{I am a teenager} \end{array} \]
\[ \begin{array}{c@{\,}l@{}} & \text{I am 18}\\ & \text{If someone is 18, they are a teenager}\\\hline \therefore & \text{I am a teenager} \end{array} \]
| I am 18 (\(p\)) | I am a teen (\(q\)) | If I am 18, I am a teen (\(p \Rightarrow q\)) | I am a teen (\(q\)) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
What row describes our reality?
Rules of Inference
\[ \begin{array}{c@{\,}l@{}} & \text{I am 18}\\ & \text{If someone is 18, they are a teenager}\\\hline \therefore & \text{I am a teenager} \end{array} \]
Common argument structure
\[ \begin{array}{c@{\,}l@{}} & p\\ & p \Rightarrow q\\\hline \therefore & q \end{array} \]
Common argument structure
Modus Ponens
\[ \begin{array}{rl} & \fragment{1}{\text{I am not a teenager}}\\ & \fragment{2}{\text{If someone is 18, they are a teenager}}\\\hline \fragment{3}{\therefore} & \fragment{3}{\text{I am not 18}} \end{array} \]
\[ \begin{array}{rl} & \text{~}q\\ & p \Rightarrow q\\\hline \therefore & \text{~}p \end{array} \]
Modus Tollens
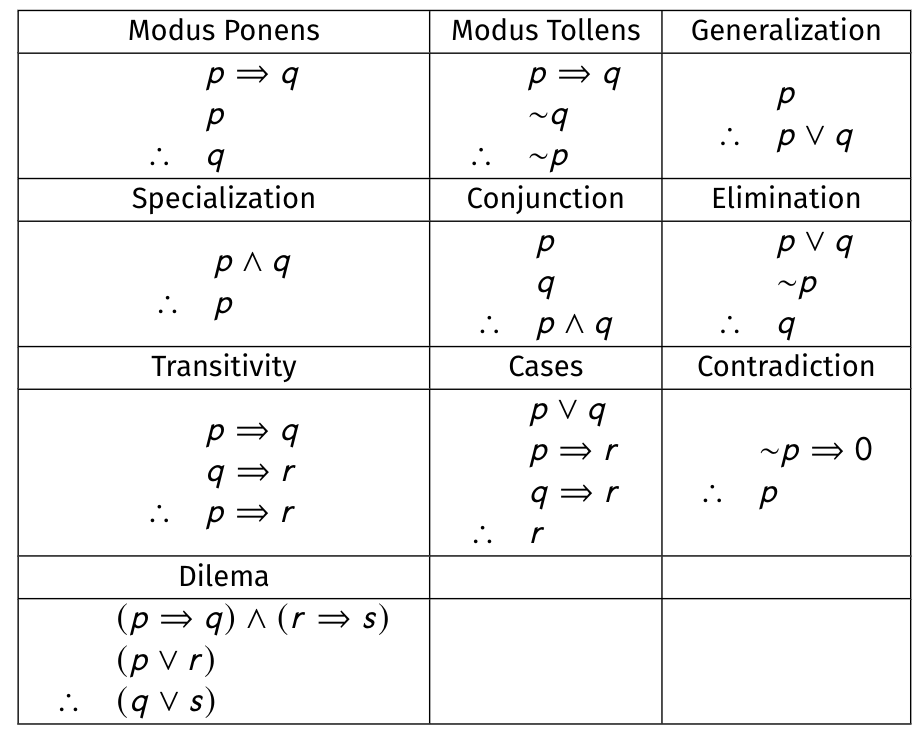

\[ \begin{array}{rl} & p\\ & p \Rightarrow q\\ & q \Rightarrow r\\\hline \therefore & r \end{array} \]
\[ \begin{array}{rll} \fragment{1}{(1)}& p &\\ \fragment{1}{(2)}& p \Rightarrow q &\\ \fragment{1}{(3)}& q \Rightarrow r &\\ \fragment{2}{(4)}& \fragment{2}{q} & \fragment{3}{\text{Modus Ponens (1,2)}}\\\hline \fragment{4}{\therefore}& \fragment{4}{r} & \fragment{5}{\text{Modus Ponens (3,4)}}\\ \end{array} \]

\[ \begin{array}{rl} & p \lor q\\ & q \Rightarrow r\\ & (p \land s) \Rightarrow t\\ & {\sim} r\\ & ({\sim} q) \Rightarrow (u \land s)\\\hline \therefore & t \end{array} \]
\[ \begin{array}{rll} \fragment{1}{\text{(1)}} & p \lor q & \\ \fragment{1}{\text{(2)}} & q \Rightarrow r & \\ \fragment{1}{\text{(3)}} & (p \land s) \Rightarrow t & \\ \fragment{1}{\text{(4)}} & {\sim}r & \\ \fragment{1}{\text{(5)}} & ({\sim}q) \Rightarrow (u \land s) & \\ \end{array} \]
\[ \begin{array}{rll} \fragment{2}{\text{(6)}} & \fragment{2}{{\sim} q} & \fragment{3}{\text{Modus Ponens (2,4)}}\\ \fragment{4}{\text{(7)}} & \fragment{4}{p} & \fragment{5}{\text{Eliminiation (1,6)}}\\ \fragment{6}{\text{(8)}} & \fragment{6}{u \land s} & \fragment{7}{\text{Modus Ponens (5,6)}}\\ \fragment{8}{\text{(9)}} & \fragment{8}{s} & \fragment{9}{\text{Specialization (8)}}\\ \fragment{10}{\text{(10)}} & \fragment{10}{p \land s} & \fragment{11}{\text{Conjunction (7,9)}}\\\hline \fragment{12}{\therefore} & \fragment{12}{t} & \fragment{13}{\text{Modus Ponens (3,10)}}\\ \end{array} \]
\[ \begin{array}{rll} {\text{(1)}} & p \lor q & \\ {\text{(2)}} & q \Rightarrow r & \\ {\text{(3)}} & (p \land s) \Rightarrow t & \\ {\text{(4)}} & {\sim}r & \\ {\text{(5)}} & ({\sim}q) \Rightarrow (u \land s) & \\ \end{array} \]
\[ \begin{array}{rll} {\text{(6)}} & {{\sim} q} & {\text{Modus Tollens (2,4)}}\\ {\text{(7)}} & {p} & {\text{Eliminiation (1,6)}}\\ {\text{(8)}} & {u \land s} & {\text{Modus Ponens (5,6)}}\\ {\text{(9)}} & {s} & {\text{Specialization (8)}}\\ {\text{(10)}} & {p \land s} & {\text{Conjunction (7,9)}}\\\hline {\therefore} & {t} & {\text{Modus Ponens (3,10)}}\\ \end{array} \]
Style: all to be on new lines, just ran out of space here