CMSC250
Logic
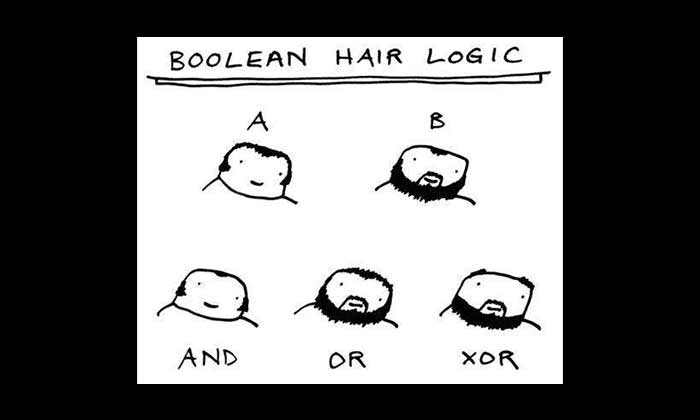
Logic
Statements
Statement: a declarative sentence with a truth value
ie. A sentence that is either true or false, but not both
Aristotle's work founded Aristotelian logic
Discrete Math has no applications to CS
\[2 + 2 = 4\]
\[1 + 1 = 0\]
They are not opinions
C is better programming language than Java
They are not meaningless
Colorless green ideas sleep furiously
Must be defined
\[x > 30\]
Must be defined
let \(x\) be the number of students in class
\[x > 30\]
Statements variables are denoted as a lowercase letter
\[x > 30\]
\(y\): there are more than 30 students in the class
Operations
Statements can be modified and combined
- Negation: \(\neg, {\sim}, \bar p\)
- Conjunction: \(\land\)
- Disjunction: \(\lor\)
- Implication: \(\Rightarrow\)
Negation
I have graduated highschool
I have not graduated highschool
!(I have graduated highschool)
~(I have graduated highschool)
\(p: 2 + 2 = 4\)
~\(p:\)~\(( 2 + 2 = 4)\)
\(p: 2 + 2 = 4\)
~\(p:\)~\(( 2 + 2 = 4)\)
\[ \text{~}p = \begin{cases} \text{true} & \text{if } p \text{ is false}\\ \text{false} & \text{if } p \text{ is true}\\ \end{cases} \]Conjunction
\(p\): Tomorrow will be cloudy
\(q\): Tomorrow will be sunny
Tomorrow will be cloudy and sunny
\(p\) && \(q\)
\(p \land q\)
\(p\): Tomorrow will be cloudy
\(q\): Tomorrow will be sunny
\(p \land q\)
\[ p \land q = \begin{cases} \text{true} & \text{if both of } p \text{ and } q \text{ is True}\\ \text{false} & \text{if one or both of } p \text{ and } q \text{ is false}\\ \end{cases} \]\(p\): \(2 + 2 = 4\)
\(q\): \(4 + 2 = 6\)
\(p \land q\)
\(p\): \(2 + 2 = 5\)
\(q\): \(1 + 2 = 3\)
\(p \land q\)
Disjunction
\(p\): Tomorrow will be cloudy
\(q\): Tomorrow will be sunny
Tomorrow will be cloudy or sunny
\(p || q\)
\(p \lor q\)
\(p\): Tomorrow will be cloudy
\(q\): Tomorrow will be sunny
\(p \lor q\)
\[ p \lor q = \begin{cases} \text{true} & \text{if one or both of } p \text{ and } q \text{ is true}\\ \text{false} & \text{if } p \text{ is false and } q \text{ is false}\\ \end{cases} \]\(p\): \(2 + 2 = 4\)
\(q\): \(4 + 5 = 1\)
\(p \lor q\)
\(p\): \(2 + 2 = 5\)
\(q\): \(1 + 2 = 4\)
\(p \lor q\)
Note: Logical OR is not the same as English OR
I am younger than 50 or I am at least 50
I am having fun or I am causing chaos
Note: Logical OR is not the same as English OR
I am younger than 50 \(\oplus\) I am at least 50
I am having fun \(\lor \) I am causing chaos
Note: Logical OR is not the same as English OR
I am younger than 50 \(\oplus\) I am at least 50
I am having fun \(\lor \) I am causing chaos
\(\oplus\) is exclusive or
Can make with and, or and not so we will not be using them in this class
\(\oplus\) is exclusive or
Can make with and, or and not so we will not be using them in this class
\(p \oplus q\):\((p \lor q) \land ({\sim}(p \land q))\)
Implication
\(p\): I throw a ball
\(q\): The window will break
\(p \Rightarrow q\)
This is not causal
This is not causal
\(p\): The sky is blue
\(q\): 2 + 2 = 4
\(p \Rightarrow q\)
Conditionals are tricky
They are true if the antecedent is false \(\lor\) the consequent is true
Truth Tables can help visualize this
Truth Tables and Equivalence
We may want to make really long statements
Truth Tables
| \(p\) | ~\(p\) |
|---|---|
| 0 | 1 |
| 1 | 0 |
| \(p\) | \(q\) | \(p \lor q\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| \(p\) | \(q\) | \(p \land q\) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| \(p\) | \(q\) | \(p \Rightarrow q\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Think of this as a promise between \(p\) and \(q\)
| \(p\) | \(q\) | \(p \Rightarrow q\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
\((p \Leftrightarrow q) \equiv ((p \Rightarrow q)\land(q \Rightarrow p)\)
Read as: p iff q, p if and only if q
| \(p\) | \(q\) | \(p \Rightarrow q\) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
We can rewrite with \(\land,\lor,{\sim}\): \(({\sim}p) \lor q\)
| \(p\) | \(q\) | ~\(p\) | \({(\sim}p) \lor q\) |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| \(p\) | \(q\) | \(r\) | \(p \lor q\) | ~\(r\) | \((p \lor q) \land (\)~\(r)\) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
Equivalence
Note: Two statements \(p\) and \(q\) are logically equivalent \((p \equiv q)\)when they have the same T/F value for all value combinations
Note: Two statements \(p\) and \(q\) are logically equivalent \((p \equiv q)\)when they have the same T/F value for all value combinations
ie. They have the same truth table
\(p \equiv\)~\((\)~\(p)\)
| \(p\) | ~\(p\) | ~\((\)~\(p)\) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
\((p \Rightarrow q) \equiv (({\sim}p) \lor q)\)
| \(p\) | \(q\) | \(\sim p\) | \(p \Rightarrow q\) | \((({\sim}p) \lor q)\) |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
\((p \Rightarrow q) \equiv (({\sim}p) \lor q)\)
\((p \Rightarrow q) \equiv(q \Rightarrow p)\)?
\((p \Rightarrow q) \equiv(({\sim}p) \Rightarrow ({\sim}q))\)?
\((p \Rightarrow q) \equiv(({\sim}q) \Rightarrow ({\sim}p))\)?
\((p \Rightarrow q) \equiv (({\sim}p) \lor q)\)
\((p \Rightarrow q) \equiv(q \Rightarrow p)\)?
(converse)
\((p \Rightarrow q) \equiv(({\sim}p) \Rightarrow ({\sim}q))\)?
(inverse)
\((p \Rightarrow q) \equiv(({\sim}q) \Rightarrow ({\sim}p))\)?
(Contrapositive)
\((p \Rightarrow q),(q \Rightarrow p),(({\sim}p)\Rightarrow {\sim}q), (({\sim}q) \Rightarrow ({\sim}p))\)
| \(p\) | \(q\) | \(p \Rightarrow q\) | \(q \Rightarrow p\) | \(({\sim}p) \Rightarrow ({\sim} q)\) | \(({\sim}q) \Rightarrow ({\sim} p)\) |
|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
~\((p \lor q) \equiv (\)~\(p)\land (\)~\(q)\)
~\((p \lor q) \equiv (\)~\(p)\land (\)~\(q)\)
| \(p\) | \(q\) | ~\(p\) | ~\(q\) | \(p \lor q\) | ~\((p \lor q)\) | \((\)~\(p)\land(\)~\(q)\) |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
~\((p \lor q) \equiv (\)~\(p)\land (\)~\(q)\)
~\((p \land q) \equiv (\)~\(p)\lor (\)~\(q)\)
Note: These together are known as DeMorgan's Laws
Note a few special Cases
Note a few special Cases
| \(p\) | ~\(p\) | ~\(p \lor p\) |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 0 | 1 |
Tautology
| \(p\) | ~\(p\) | ~\(p \land p\) |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 0 |
Contradiction